サイト内検索
分子研について
研究情報
共同利用案内
- 共同研究・施設利用案内
- 申請概要
- 共同研究受入研究室・利用装置一覧
- WEB申請
大学院
- 大学院教育
- 大学院案内
- 受験生向け情報
- 他大学の学生の受け入れ
- 在校生向け情報

タンパク質とはアミノ酸が1 次元的に(枝分かれすることなく)つながったひもである。生体中でタンパク質はαへリックスやβシートなどの立体的な構造をとっている。天然のアミノ酸には20 種類あり、これらのアミノ酸がどう並ぶかでタンパク質の安定な立体構造は変わる。アミノ酸の1 次元配列情報からタンパク質の立体構造を理論的に予測する問題を「タンパク質の折りたたみ問題」と言う(図1)。この問題が注目されている理由の1つは、理論物理学の手法でタンパク質の折りたたみという生物の問題を説明できるのか?という基礎科学的な興味である。またもう1つの理由は、タンパク質が間違って折りたたむことにより発病する病気の原因解明と、その治療に役立てられるのではないかという医学的応用に向けたものである。
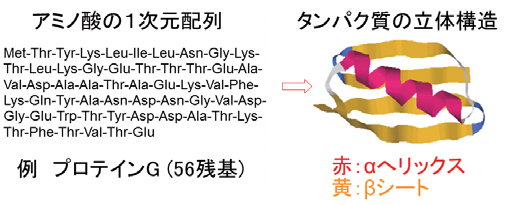
図1 タンパク質の折りたたみ問題。
分子動力学シミュレーションは、コンピューター上で仮想的に原子や分子を配置し、その運動を調べる理論的手法である。しかし、タンパク質などの生体分子には自由エネルギー曲面に多
くの極小値があるため(図2)、通常の分子動力学シミュレーションを行ったのではこれらの極小値にトラップされてしまい、正しく構造を探索することができない。この問題を解決するために、マルチカノニカル法やレプリカ交換法などの拡張アンサンブル法と総称される手法が提案されてきた[1]。本稿では我々が開発してきた拡張アンサンブル法や、拡張アンサンブル法を用いたタンパク質の構造変化の研究、さらにタンパク質が間違って折りたたみ凝集することによってできるアミロイド線維に関するシミュレーションについて紹介する。
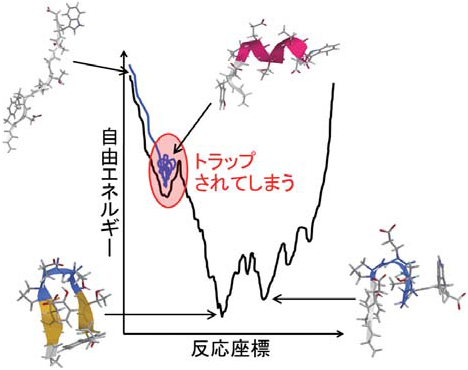 図2 タンパク質の自由エネルギーの概念図。単純に分子動力学シミュレーションを行うと途中にある極小状態にトラップされて最安定状態にたどり着けない。
図2 タンパク質の自由エネルギーの概念図。単純に分子動力学シミュレーションを行うと途中にある極小状態にトラップされて最安定状態にたどり着けない。
拡張アンサンブル法の代表的手法であるレプリカ交換法[2,3] では、系のコピー(レプリカ)を複数用意し、シミュレーションの途中で図3(a) のように2つのレプリカ間で温度を交換するか否か判定する。このように各レプリカの温度を上下させることで、自由エネルギー極小状態に捕らわれることなく効率的な構造空間のサンプリングを実現できる。温度交換の際には、代表的なモンテカルロ法であるメトロポリス法[4] を用いて温度を交換するか否か判定し、正しい統計アンサンブル(カノニカルアンサンブル)を実現させる。メトロポリス法ではモンテカルロ法の試行がアクセプトされないことがあるが、最近、モンテカルロ法の試行がほぼ確実にアクセプトされる新しいモンテカルロ法「諏訪・藤堂法」が提案された[5]。ただし、モンテカルロ法における状態が2 つしかない場合には、諏訪・藤堂法とメトロポリス法は等価になっ
てしまう。レプリカ交換の枠組みでは、温度を交換するかしないかの2 つの状態しかないので、このままでは諏訪・藤堂法の利点を活かせない。そこで図3(b) のように3 つ以上の系の間で温度を置換する新しい手法「レプリカ置換法」を考案した[6]。レプリカ置換法では従来のレプリカ交換法よりも温度を2倍程度効率よく遷移させることができるし、構造空間もより効率よく探索できることが分かった。
この方法を用いてC ペプチドの折りたたみシミュレーションを行った。このペプチドはGlu2 の酸素原子とArg10の水素原子が塩橋を作ることでαへリックス構造を安定化させることが知られている。自由エネルギー地形(図4(a))を計算し、伸びた状態F から、まずGlu2 とArg10 が近づいて塩橋を形成し(状態B)、その後αへリックス構造を形成し折りたたんだ状態A に至ることを明らかにした(図4(b))[6]。
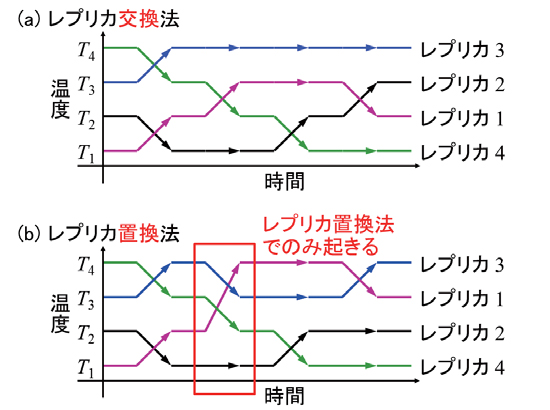 図3 (a) レプリカ交換法と(b) レプリカ置換法。レプリカ交換法では2 つのレプリカの間で温度を交換するのに対し、レプリカ置換法では3 つ以上のレプリカの間で温度を置換する。
図3 (a) レプリカ交換法と(b) レプリカ置換法。レプリカ交換法では2 つのレプリカの間で温度を交換するのに対し、レプリカ置換法では3 つ以上のレプリカの間で温度を置換する。
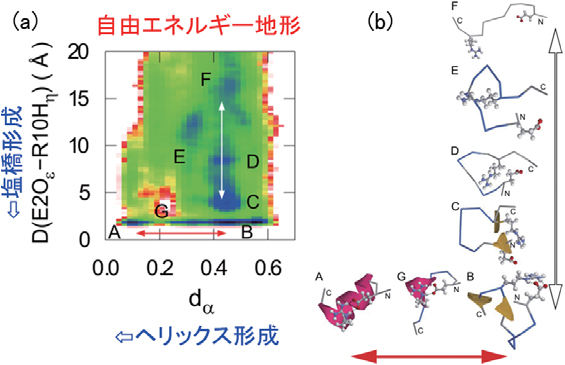
図4 C ペプチドの(a) 自由エネルギー地形と(b) 各自由エネルギー極小状態における典型的な
構造。自由エネルギー地形の横軸は理想的なαへリックス構造からどれくらい離れているか
を表し、縦軸は塩橋を作るGlu2 の酸素原子とArg10 の水素原子の距離である。
タンパク質は温度や圧力などの環境が変わると変性する。拡張アンサンブル法は、温度や圧力が変化した際にタンパク質の構造がどのように変化するかを調べるのにも活用できる。通常、
タンパク質は圧力をかけると変性し、ほどけてしまう[7]。ところが、AK16ペプチドでは圧力をかけると逆にαへリックス構造の形成率が増えることが最近の実験で示された(図5(a))[8]。そこで我々は拡張アンサンブル法のひとつである、温度・圧力に関する焼き戻し法[9] を用いて、AK16 ペプチドの構造の圧力依存性を調べた。その結果、圧力の増加にともない、αヘリックス構造の割合は途中までは減少するが、その後増加した。高圧力側だけでとはいえ、圧力によりαヘリックス構造が増えるという実験結果を再現できたのはこれが初めてである。さらに慣性半径を計算したところ、図5(b) のようにαヘリックス構造の慣性半径は圧力とともに減少するのに対し、アンフォールド状態の慣性半径はほとんど変化ないことがわかった。このことからαヘリックス構造は加圧にともない縮むために、高圧力条件下ではαヘリックス構造が増えることを明らかにした[10,11]。
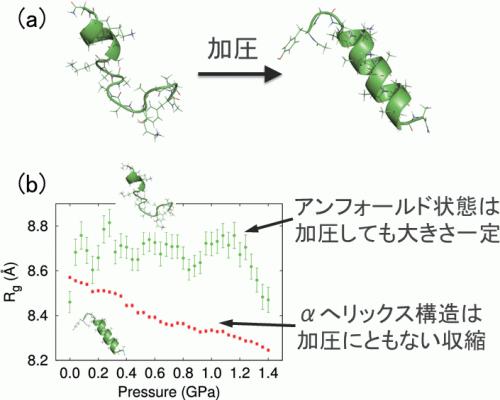 図5 (a)AK16 ペプチドは加圧により、より多くのαヘリックス構造を取ることが知られている。(b)AK16 ペプチドのαヘリックス構造は加圧により収縮する。
図5 (a)AK16 ペプチドは加圧により、より多くのαヘリックス構造を取ることが知られている。(b)AK16 ペプチドのαヘリックス構造は加圧により収縮する。
タンパク質は溶液中の濃度が高くなるとアミロイド線維を形成することがある。アミロイド線維は、タンパク質が間違って折りたたみ、凝集することによってできた不溶性の線維である。
アミロイド線維は20 種類以上の病気の原因と考えられている。例えばアルツハイマー病はアミロイドβペプチドが凝集してできたアミロイド線維が原因ではないかと言われている。しかし、アミロイド線維の形成メカニズムはまだわかっていない。そこでレプリカ置換法の1 つである、クーロンレプリカ置換法を使ってアミロイドβペプチドのフラグメントAβ(29-42) の2 量体形成機構を調べた[12,13]。クーロンレプリカ置換法では電荷をスケールするパラメーターを導入し、温度の代わりにこのパラメーターをレプリカ間で置換することにより、2 つの分子を近づけたり遠ざけたりできる。その結果、図6(a) のように2 つのAβ(29-42) が離れている状態F から近づくにつれ、まず疎水性残基の多いC 末部分で短い分子間βシート構造を形成し(状態D)、その後βシート構造を形成する残基が増えて、最終的に長い反平行βシート構造(状態A)を作ることが明らかになった[12]。さらに、分子間βシート構造を作る直前には、図6(b) のように分子内でのβシート構造(βヘアピン構造)が増え、それはもう一方の分子の疎水性残基が接触することにより安定化されていることも発見した(図6(c))[13]。
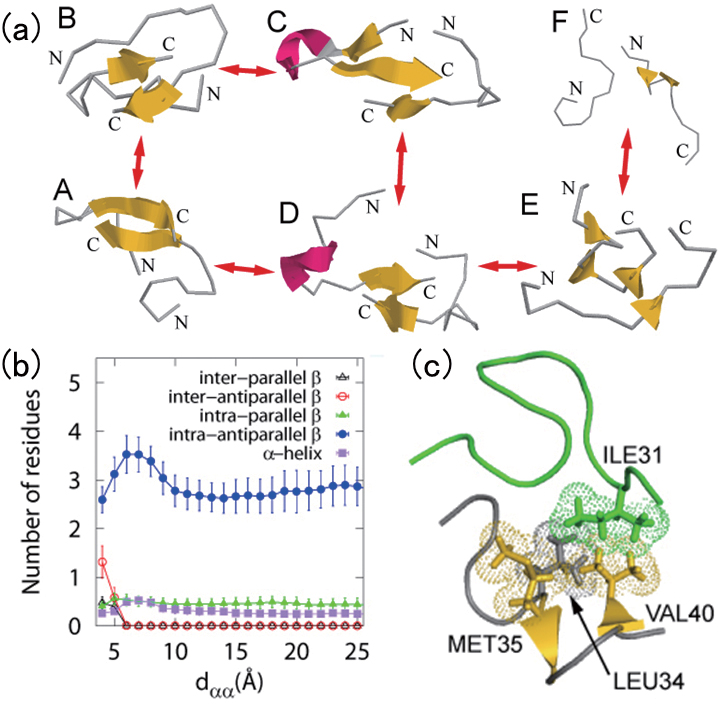 図6 (a)アミロイドβペプチドのフラグメントの2量体化過程。(b)分子間距離dαα と各種2次構
図6 (a)アミロイドβペプチドのフラグメントの2量体化過程。(b)分子間距離dαα と各種2次構
造を取る残基数の関係。(c) 分子間βシート構造を作る直前に分子内βシート構造をもう一方の分子の疎水性残基が安定化させている。
近年、超音波を使ってアミロイド線維を破壊する実験報告がいくつかなされている。その破壊メカニズムはキャビテーション(気泡生成)によるものではないかと指摘されているが、水中
の気泡がどのようにアミロイド線維を破壊するのか、原子レベルでの詳細は分かっていない。そこで我々はアミロイドβペプチドからなるアミロイド線維に超音波をかけた非平衡分子動力学シミュレーションを行った[14]。その結果を図7 に示す。圧力が正の時はアミロイドや水の構造に大きな変化は見られないが、負圧になった時にアミロイドの周りに気泡が生じた。この気泡は疎水性残基の周りに生じることが多かった。アミロイドの周りの水がほぼ蒸発し気泡に包まれても、アミロイドは壊れなかった。その後圧力が再び正になると、気泡が崩壊し水のジェット流がアミロイドにぶつかり、アミロイドが破壊された。この時、水は主に親水性残基めがけて飛んでいることが分かった。このように生体分子系で気体・液体の相転移を含む非平衡分子シミュレーションを行い、キャビテーションによりアミロイドβ線維の破壊過程を原子レベルで解明したのは、この研究が初めてである。
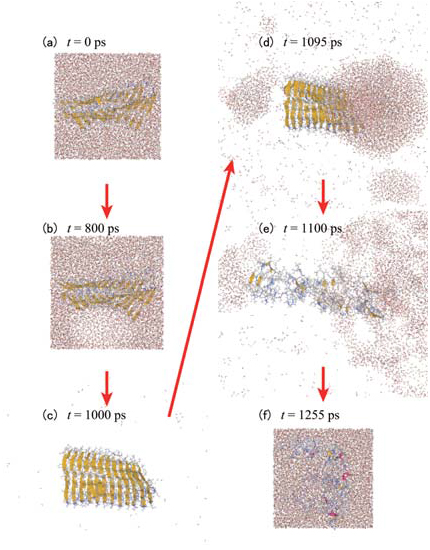 図7 超音波によるアミロイド線維の破壊過程。気泡がつぶれるときにアミロイド線維が破壊されている。
図7 超音波によるアミロイド線維の破壊過程。気泡がつぶれるときにアミロイド線維が破壊されている。
分子動力学シミュレーションは生体分子の運動を解明する強力なツールである。もともと分子動力学シミュレーションは今から60年近く前に、固体・流体相転移の研究として始まったが、今日では物理学や化学だけでなく、生物、医学への応用にも使われている。筆者自身、学生の頃物理学を専攻し、今でも物理学を基礎に新しい分子動力学法の開発に取り組む一方、最近ではアミロイド病など医学的なテーマへの応用にも興味を持っている。今後も分子科学の立場から、医学・薬学への応用にも積極的に取り組んでいきたい。ここで紹介した研究は伊藤暁助教、森義治特任助教との共同研究の成果である。彼らの協力に感謝する。また、これらの研究は科学研究費補助金(23740325 および26102550)、岡崎オリオンプロジェクトの助成を受けて行われた。シミュレーションの実行には計算科学研究センターのスパコンを利用した。
[1] A. Mitsutake, Y. Sugita, and Y. Okamoto: Biopolymers 60 (2001) 96−123.
[2] K. Hukushima and K. Nemoto: J. Phys. Soc. Jpn. 65 (1996) 1604−1608.
[3] Y. Sugita and Y. Okamoto: Chem. Phys. Lett. 314 (1999) 141−151.
[4] N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller: J. Chem. Phys. 21 (1953) 1087−1092.
[5] H. Suwa and S. Todo: Phys. Rev. Lett. 105 (2010) 120603.
[6] S. G. Itoh and H. Okumura: J. Chem. Theory Comput. 9 (2013) 570−581.
[7] H. Okumura: Proteins 80 (2012) 2397−2416.
[8] T. Takekiyo, A. Shimizu, M. Kato, Y. Taniguchi: Biochim. Biophys. Acta 1750 (2005) 1−4.
[9] Y. Mori and Y. Okamoto: J. Phys. Soc. Jpn. 79 (2010) 074003.
[10] Y. Mori and H. Okumura: J. Phys. Chem. Lett. 4 (2013) 2079−2083.
[11] Y. Mori and H. Okumura: Proteins 82 (2014), in press.
[12] S. G. Itoh and H. Okumura: J. Comput. Chem. 34 (2013) 2493−2497.
[13] S. G. Itoh and H. Okumura: J. Phys. Chem. B, in press.
[14] H. Okumura and S. G. Itoh: J. Am. Chem. Soc. 136 (2014) 10549-10552.