ポイント

3次元（多層状）ゼロギャップ伝導体(※1)へのキャリア注入に世界で初めて成功
高易動度を実現し、低温で初めて量子輸送現象を観測
散逸(※2)が無く、環境にやさしい高易動度分子性電子デバイス開発へ期待

学校法人東邦大学（炭山嘉伸理事長）、独立行政法人理化学研究所（野依良治理事長）と自然科学研究機構分子科学研究所（大峯巖所長）は、ゼロギャップ伝導体として世界で唯一、多層構造を有する分子性伝導体α-(BEDT-TTF)₂I₃へ のキャリア注入に初めて成功し、特徴的な量子輸送現象を低温で実現しました。東邦大学理学部の田嶋尚也准教授（理化学研究所加藤分子物性研究室客員主幹研 究員）、理化学研究所の川椙義高研究員、加藤礼三主任研究員、分子科学研究所の須田理行助教、山本浩史教授等研究グループによる成果です。
近年、環境にやさしい優れた電子機能をもつ新規物質の開発とその基礎研究が強く求められています。こうした中で、研究チームは世界で初めての「3次元単結晶」ゼロギャップ伝導状態の物質を、有機導体α-(BEDT-TTF)₂I₃(※ 3・※4)に圧力をかけることによって発見しました。この物質は、特殊なエネルギー構造により、あたかも光と同様、質量がゼロであるかのように振る舞う電 子が電気伝導の主役となるために、新規の電子デバイスとして期待されます。電気抵抗の原因となる後方散乱(※5)が抑制される効果があるのも特徴の1つで す。電子デバイスに重要な物理量である易動度は低温で約10⁶ cm²/V.sと非常に高いことから、キャリアを注入することによって、エネルギーが散逸されない高速駆動電子デバイス開発が期待されます。
これまで、この物質へのキャリア注入方法がまだ確立していないこと等から、分子性ゼロギャップ伝導体によるデバイスは実現困難であると考えられていました が、今回、研究チームは、プラスチック基板に厚さ100nm程度の薄片単結晶試料を固定するだけで正孔キャリアを注入することに初めて成功しました。低温 で正孔は10⁴ cm²/V.s以上の高い易動度をもち、この系に特徴的な量子ホール効果(※6)を観測 することに成功しました。これは、このデバイスが非常に良質であることを実証したことになります。今回の成果は、分子性ゼロギャップ伝導体を用いた電子デ バイス開発に向けた大きな第一歩です。今後この成果を基にして、この系へのキャリア注入制御を確立することで新たな分子性電子デバイスの展開が期待できま す。

本研究成果は、平成25年9月１日 米国の科学雑誌『Physical Review B』に掲載されるに先立ち、８月26日（日本日付：8月27日）にオンライン版に掲載される予定です。

[研究の背景]

運動量空間で伝導帯と価電子帯との間のエネルギーギャップがゼロ、つまり点(ディラック点と呼ぶ)で接しているゼ ロギャップ伝導体が2005年にガイム等(マンチェスター大学)が層状構造をしているグラファイトを1層だけにしたグラフェンで実現し、大変話題になりま した。発見から異例の速さでガイム等は2010年にノーベル物理学賞を受賞しました。
その理由はディラック点付近の特殊なバンド構造にあります。ゼロギャップ伝導体ではバンド構造の特殊性によって、光と同様、質量ゼロの電子が固体の中で振 舞い、電気伝導の主役を演じることを、ガイム等は通常の金属や半導体では見られない特殊な電気伝導特性や新奇の量子効果によって示しました。応用の面で も、高速駆動の電子デバイス展開が期待されています。
一方、今回の研究チームはグラフェンの発見とほぼ同時期に高圧下にある分子性導体α-(BEDT-TTF)₂I₃ (図1)が世界唯一のバルクな（多層状）ゼロギャップ伝導体であることを発見しました。図2(左図)に示すように、ディラック点近傍では2つの円錐型バン ドが上下から角突き合わせたゼロギャップ構造をしています。このエネルギー構造の特殊性により、質量ゼロの電子が実現し、その後方散乱が抑制されることを 実験的に実証してきました(2009年4月30日理化学研究所プレスリリース)。さらに、電子デバイスに最も重要な物理量であるキャリア易動度は低温で約 10⁶ cm²/V.sと非常に高いことが明らかです。従って、この物質を舞台にしてエネルギーが散逸され ない高速駆動の電子デバイス実現が期待されています。低コストで環境に優しい（グリーンである）など、次世代に期待される優れた機能をもつ電子デバイス開 発に向けて重要な素養を持ちます。

デバイス化するには、電子や正孔を注入したときに電気的性質が大きく変化することが求められます。しかし、この物 質へのキャリア注入方法はまだ確立していませんでした。これまで研究チームはSi基板等を利用した通常の電界効果(※7)トランジスタ（FET）を作製 し、この物質へのキャリア注入を挑戦してきました。しかし、基板と試料の圧力や熱による歪（収縮・膨張率）の違いが問題となり、この物質へのキャリア注入 は成功していませんでした。さらに、通常の電界キャリア注入は界面でのみ起こるために、電気伝導性が高い単結晶であることがキャリア注入効果を弱めます。 これらの理由により、分子性ゼロギャップ伝導体によるデバイスは実現困難であるとこれまで考えられていました。

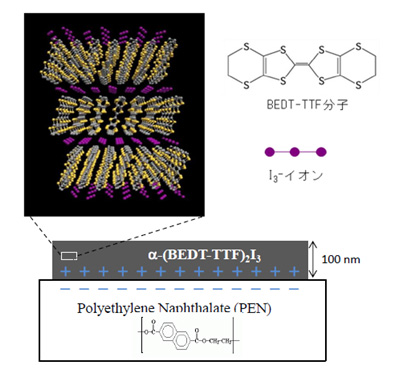
図1 有機導体α-(BEDT-TTF)₂I₃の結晶構造とプラスチックPENデバイス

負に帯電したPEN基板上に試料を固定することで、正孔を注入することに成功した。このキャリア注入方法を接触帯電法という。

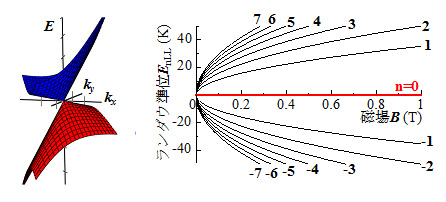
図2 高圧下におけるα-(BEDT-TTF)₂I₃のゼロギャップ構造(左)とランダウ準位(右)

[研究手法]

分子性ゼロギャップ伝導体α-(BEDT-TTF)₂I₃のFET駆動を目指し、研究チームは以下に述べる簡単な手法でキャリア注入を試みました。
この物質は低温で、1層あたりのキャリア濃度は10⁸ cm^-2と非常に低く、ヘリウム液面上の電子濃度に匹敵する値です。従って、わずかに負に帯電した基板に試料を固定しただけで、接触帯電法による正孔注入の効果を電気伝導性に検出されると期待できます。
ここで、この手法の主な問題点及び対策等を以下に記述します。
(1)　通常の電界キャリア注入は界面のみで起こります。そこで、この効果を検出するために約100nmの厚みの薄片結晶を用いました。
(2)　薄片結晶は基板上に固定しますが、基板と試料の圧力や熱による歪（収縮・膨張率）の違いが問題となります。本研究では、歪効果が有機導体とかけ離れていないプラスチックPEN基板に試料を固定しました(図1)。
(3)　 (2)の理由から、プラスチック基板上に固定した試料でも高圧力下でゼロギャップ電子系が実現するかどうかということを実証する必要があります。実際に実 験を行ったところ、ゼロギャップ電子系に特徴的な量子輸送現象を観測することに成功しました。

以上の方法で、分子性ゼロギャップ電子系α-(BEDT-TTF)₂I₃への正孔注入を実現させ、磁気抵抗効果とホール効果等からこのデバイスの評価を行いました。

[研究成果]

通常、磁場をかけると固体中の電子のエネルギーはとびとびの値しかとれなくなります。 これをランダウ準位(※8)と呼びます。ゼロギャップ伝導体では、通常の導体とは異なるランダウ準位構造[図2(右図)]をとることが知られています。ゼ ロモードと呼ばれる特別なランダウ準位がディラック点の位置に常に現れることも特徴です。本研究の最も重要な成果は、図3に示すようにゼロギャップ電子系 特有のランダウ準位構造に起因した量子磁気抵抗振動(シュブニコフ・ド・ハース振動：SdH振動) (※9)と量子ホール効果(QHE)を分子性ゼロギャップ電子系では初めて観測したことです。ゼロギャップ電子系では、キャリアを注入しなければフェルミ エネルギーは常にディラック点に位置しているので、SdH振動やQHEを観測することはできません。従って、この観測はキャリア注入が成功したことを意味 しています。
以下がこのデバイスの評価結果です。
キャリア注入効果(キャリア濃度分布)をSdH振動解析から評価できます。フーリエ解析から2種類の振動成分があることが判明しました。SdH振動の位相 を調べればSdH振動起源のキャリアが通常の電子か質量ゼロの電子かを知ることが出来ます。その結果、2つの振動の起源は両方とも質量ゼロの電子であり、 このことは接触帯電法によるキャリア注入が成功したことを強く示唆します。このデバイスのキャリア濃度分布を解析することによって、図4のように界面から 2層目まで正孔が注入されたと推察されます。第1層目と第2層目の正孔濃度は、それぞれ3.5×10¹³ cm^-2および0.5×10¹³ cm^-2と、SdH振動の周期から見積られました。

一方、磁気抵抗振動が極小を示すところでホール抵抗がプラトーを示すのがQHEの特徴です。詳細な解析から、ゼロ ギャップ電子系に特徴的な量子ステップを持つことが明らかになりました。QHEはキャリア易動度が非常に高くないと観測できません。従って、今回の結果か ら、このデバイスは非常に良質であることがわかります。

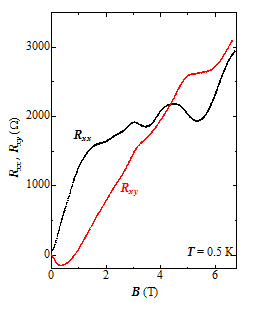
図3　0.5 Kにおける電気抵抗R_xxとホール抵抗R_xyの磁場依存性

R_xxに見られる振動はシュブニコフ・ド・ハース振動である。 R_xxが極小になるところでR_xyのプラトー(3.5 Tと5.5 T近傍)が見られるが、これが量子ホール効果の特徴である。

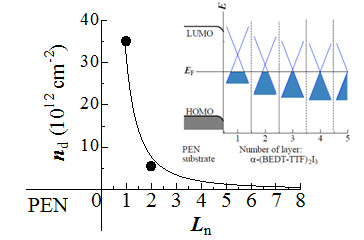
図４PENデバイスのキャリア濃度分布とエネルギーダイアグラムの略図(挿入図)

図1に示したBEDT-TTF分子層とI₃^-アニオン層のペアを1組の層として、キャリア濃度はPEN基板からの層数に対してプロットしてある。エネルギーダイアグラムは、キャリア濃度分布を基にそれぞれの層に関するエネルギースペクトル(ディラックコーン)が描かれてある。

[今後の期待]

分子性物質は構成分子が常温で自己組織的に集合して合成されるため、高温で作られるグラフェンよりもより低エネル ギーかつマイルドな条件でデバイスを作ることが出来ます。今回の成果から、分子性ゼロギャップ伝導体のFET駆動には基板と試料の圧力や熱による歪（収 縮・膨張率）の違いを小さくすることが最も重要であることが明らかになりました。この違いが大きいと、静電キャリアは界面にトラップされやすくなるために FET駆動が作動しなくなると推察されます。今回のように、試料と基板との相性が良ければ、接触帯電による僅かなキャリア注入量でも電気伝導性に大きな効 果が得ることができます。今後、分子性ゼロギャップ伝導体を用いた散逸のないグリーンなFETデバイスへの展開が期待されます。

[用語解説]

※１　ゼロギャップ伝導体
半導体のうち伝導帯と価電子帯間のエネルギーギャップが狭いものをナローギャップ半導体と呼ぶ。一般にはエネルギーギャップが0～0.5 eVの半導体に対して使われている。エネルギーギャップが狭いことが伝導帯と価電子帯の形状を鋭くし、電子または正孔の有効質量は小さくなり、高い易動度 をもつことが知られている。このエネルギーギャップがゼロで伝導帯と価電子帯が点(コンタクトポイント)で接しているものがゼロギャップ伝導体である。特 別な構造をしているために、電子の質量は見かけ上、素粒子のニュ－トリノのようにゼロである。

※２　散逸
電流エネルギーが散乱過程（電気抵抗）を通して熱に変化する現象。

※３　有機導体
有機物は、生体、樹脂、化学繊維などのように電気を通さない絶縁体である、というのが常識的な考えであった。しかし、1940年代頃から有機伝導体の開発 が行われており、1954年に東京大学理学部の赤松氏、井口氏、松永氏等が、ベンゼン環5個からなるペリレン分子と臭素とを反応させて生じた物質が高い伝 導度をもつとことを見いだした。1973年には、TCNQ (tetracynoquinodimetance)とTTF (tetrathiafulvalene)という有機分子の間で電子のやり取りをして形成される電荷移動錯体の電子状態が金属的であることが確認され、金 属元素を一切含まない「金属」が誕生した。有機導体の特徴は、望みの物性を示すように分子集合体を設計する、いわゆる分子設計あるいは機能設計が可能なこ とである。多種の有機分子性導体が開発されており、無機物質と同様に絶縁体から超伝導体まで多様な物質群を形成している。

※４　有機導体α-(BEDT-TTF)₂I₃
図1に示すような結晶構造をもつ。有機分子BEDT-TTF （bis(ethylenedithio)tetrathiafulvaleneの略称）が並んだ層とI₃^－イオンが並んだ層とが交互に積層した層状構造をしている。BEDT-TTF分子2個あたり1個の電子がI₃分子に移動し、I₃分子は閉殻となるためにI₃^－イ オン層は絶縁層である。一方、BEDT-TTF分子層は電子を放出したことで正孔ができて電気を流す。このようにして二次元電子系が形成されている。ギリ シャ文字αはBEDT-TTF分子の配列の仕方を表し、他にβ、θ、κ-型などがよく知られている。このような有機導体では、BEDT-TTF分子の配列 の仕方が電子物性を決定する。β、θ、κ-型の(BEDT-TTF)₂I₃は数Kで超伝導転移するのに対してα型は135 Kで電荷秩序による金属-絶縁体転移を起こす。1.5ギガパスカル以上の圧力でこの絶縁体転移は完全に抑制でき、ゼロギャップ電子系となる。

※５　後方散乱
電子の波は不純物と相互作用し、真後ろに散乱される過程を後方散乱過程という。散乱には時間をちょうど逆にした過程もあり、不純物によるポテンシャルは空 間的には不規則だが時間反転に対しては対称であるため、通常の電子の場合、2つの過程による後方への散乱波はちょうど同位相になる。この場合、同位相の2 つの波は干渉して強めあい、後方散乱の確率が増大する。しかし、ゼロギャップ電子系では、2つの過程の位相はπずれているために、2つの波は打消しあい、 後方散乱効果は抑制される。

※６　量子ホール効果(QHE)
ランダウ準位(※8)の状態密度は実際の試料では不純物の影響によってある程度の広がりを持つ。この時、フェルミ準位の下の電子は、波動関数が空間的に局在するようになる。この量子化した2次元電子系のホール伝導率はσ_xy=νe²/hで表される。このように、ホール伝導率がe²/hの整数倍で一定の値を持つようになる現象を整数量子ホール効果という。

※７　電界効果
薄膜材料に対して、絶縁体を隔てたゲート電極から静電場を加え、電子の密度を変化させることによって伝導性が制御される現象。CMOS回路などに使われて いる原理であり、例えばゲートに電圧をかけている間は薄膜に電気が流れ、ゲート電圧を切ると電気が流れなくなる。

※８　ランダウ準位
磁場中の電子は磁場と垂直な面内でサイクロトロン運動と呼ばれる円運動を行う。量子力学ではこのサイクロトロン運動が量子化され離散的なエネルギー準位に分裂する。これをランダウ準位と呼ぶ。通常の導体ではランダウ準位はћw_c(n+1/2) (n=0, 1, 2, …)で表わされる。ここでћはプランク定数である。wcはサイクロトロン振動数と呼び、磁場Bと有効質量m*を用いてw_c=eB/m*と書ける。一方、ゼロギャップ電子系ではフェルミ速度vF を使って(2eћv_F²|n|B)^1/2と書けるのが特徴である。従って、n=0の特別なランダウ準位(ゼロモード)がコンタクトポイントの位置（フェルミエネルギーの位置）に常に存在する。

※９　量子磁気抵抗振動(シュブニコフ・ド・ハース振動：SdH振動)
電気抵抗の磁場による変化を磁気抵抗と呼ぶ。磁場を強くしていき、フェルミエネルギーをランダウ準位が通過するときに生じる抵抗の振動をシュブニコフ・ ド・ハース振動という。磁場の逆数に比例して抵抗が振動する現象で、その周期はフェルミ面の極値断面積に反比例する。振動の解析から、フェルミ面、サイク ロトロン質量、散乱などを評価できる。

研究に関するお問い合わせ先

学校法人東邦大学理学部物理学科 物性物理学教室　　　　　　　　　
准教授　田嶋　尚也
TEL: 047-472-6990          　        

独立行政法人理化学研究所 加藤分子物性研究室　　　　　　　　
主任研究員　加藤　礼三
TEL: 048-467-4504   FAX: 048-462-4661

自然科学研究機構分子科学研究所 協奏分子システム研究センター
教授　山本　浩史
TEL: 0564-55-7334